我们截止到目前为止，大部分图案都是有序和有规律的，但是现实里，大部分景色都是无序和混沌的。

上面这张图，就是一个月光照在海面的景色。但是这张图，使用 Shader 画出来的。

下面这张图，也是一样：

一样是 Shader 写的。

思考点在于：

• shader 怎么表现出无序？
• 由于 shader 和数学是紧密相关的，在数学里，和这个概念接近的就是“随机”。

随机函数

在JavaScript中，我们可以使用内置的函数Math.random来模拟随机，但是，直到现在，GLSL好像还没有内置的随机函数可用，所幸，在Github上，已经有人封装了随机函数：glsl-random，来看看是什么样子的：

highp float random(vec2 co)
{
    highp float a=12.9898;
    highp float b=78.233;
    highp float c=43758.5453;
    highp float dt=dot(co.xy,vec2(a,b));
    highp float sn=mod(dt,3.14);
    return fract(sin(sn)*c);
}

注意：highp 的意思就是高精度。

这个随机函数的意义就是取sin函数偏后面的小数部分来模拟随机数。
简单解释一下这个随机函数的意义吧：

• a、b、c 这些常数值是用于生成随机数的魔法数字，通常由经验或试验得出，目的是确保生成的随机数序列具有良好的随机性。
• 这里 dot 函数计算 co 与 vec2(a, b) 的点积。点积操作将两个向量组合成一个标量值，这个值会用于后续的随机数生成。
• 使用 mod 函数对 dt 取余，除以 3.14 使得结果限制在一个较小的范围内。这一步是为了将 dt 转换为一个周期性值，从而增强随机性。
• 通过 sin 函数将 sn 转换成一个非线性值，然后乘以常数 c。fract 函数提取小数部分，使得返回值在 [0, 1) 范围内。

跟一段 chatgpt 的总结：

这个 random 函数生成一个基于输入向量 co 的伪随机数。它的原理是通过数学运算（点积、取余、正弦函数、小数部分）将输入映射到一个伪随机数，这种方法常用于着色器中生成伪随机值。

这类随机函数的优点是计算简便且不需要保存状态，适合在 GPU 着色器中使用。不过，由于其伪随机性，它并不适合高要求的随机数生成场景。

我们可以传入一个UV坐标，看看输出的效果：

void mainImage(out vec4 fragColor,in vec2 fragCoord){
    vec2 uv=fragCoord/iResolution.xy;

    float noise=random(uv);

    vec3 col=vec3(noise);
    fragColor=vec4(col,1.);
}

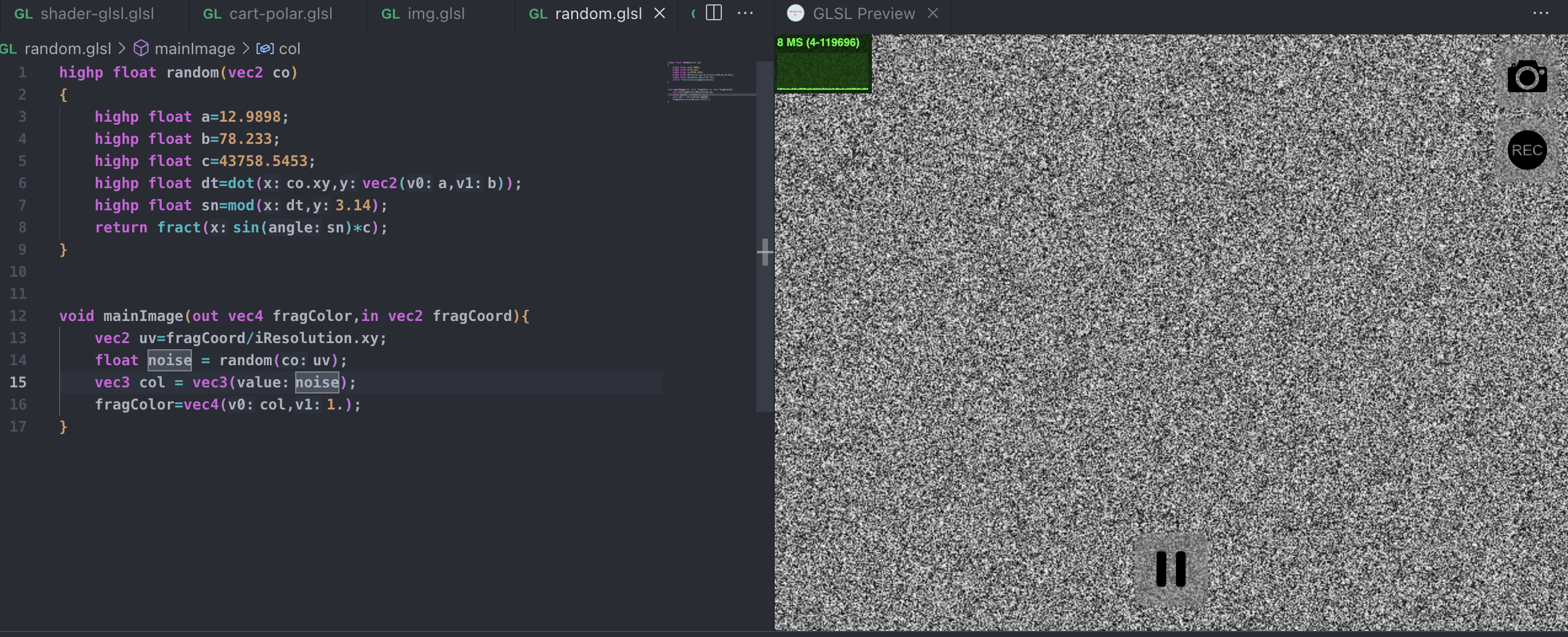
这就仿佛是一张坏掉的电视屏幕一般的噪点图。

颗粒化滤镜

如果我们将这些噪点和纹理叠加到一起，会怎么样？

我们继续使用上一篇文章的纹理图链接，给我们的纹理加上噪点：

（这里只附上一部分代码）

vec3 col=texture(iChannel0,uv).xyz;
col+=noise;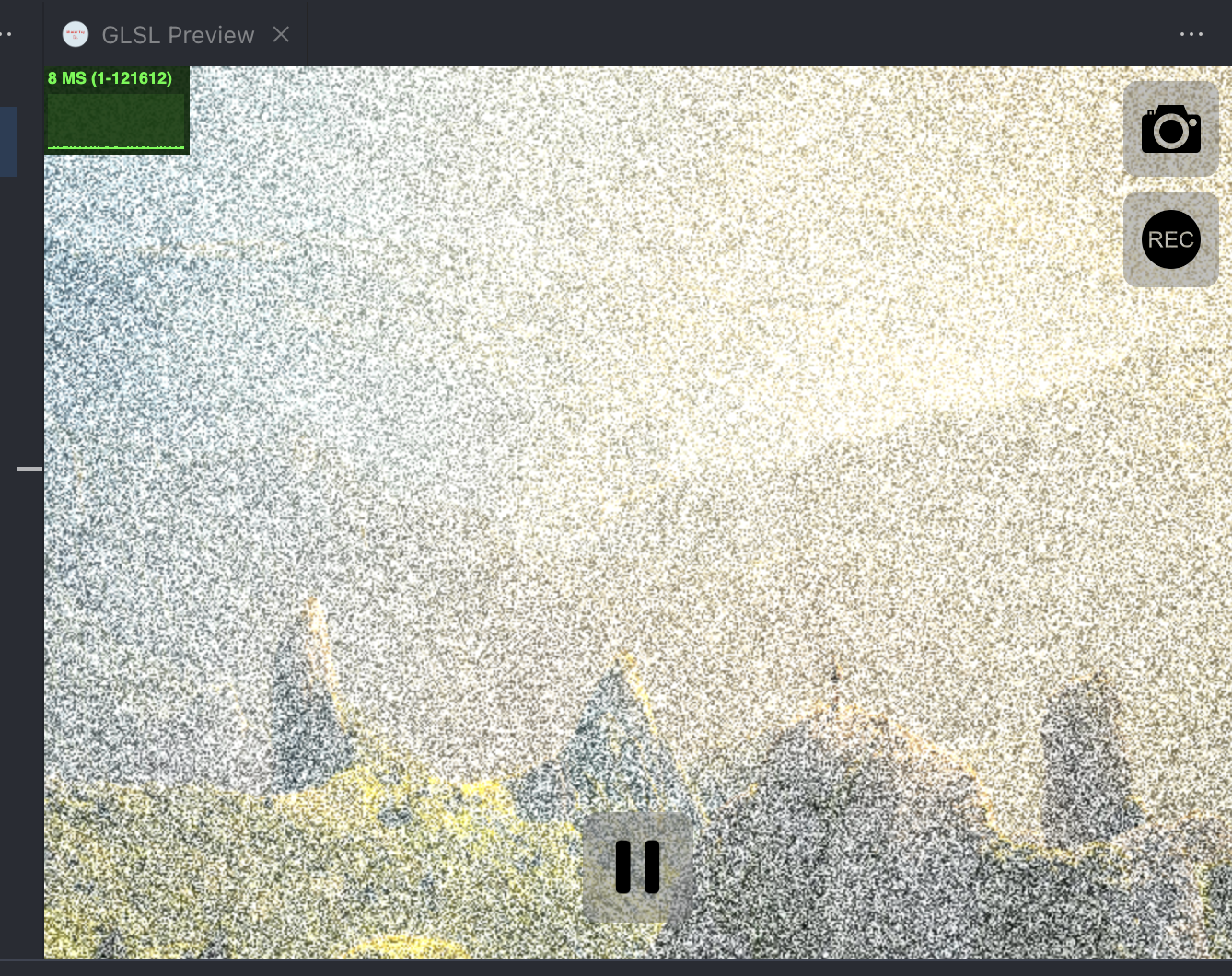

可以看到噪点的强度非常的高，怎么办呢？
我们可以给噪点降一些强度，也就是把噪点 noise 乘上一个 0.几的数值

vec3 col=texture(iChannel0,uv).xyz;
col+=noise*.2;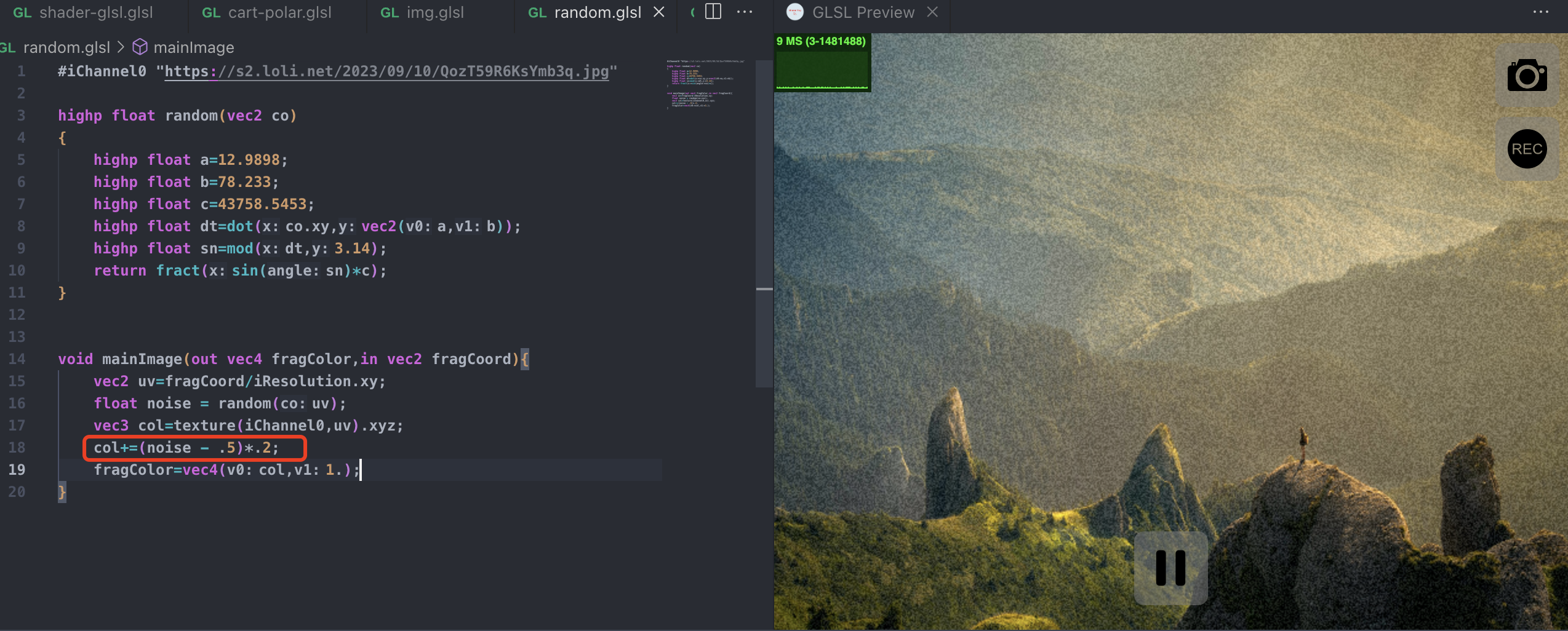

诶，这样我们就得到了一个颗粒化的滤镜的效果，如果感觉白色太明显，我们可以再减去一个 0.5

col+=(noise-.5)*.2;

直接使用 noise，那么 noise 的范围在 [0, 1)，这意味着增加的值范围是 [0, 0.2)。这样会整体上增加颜色的亮度，使得画面偏白。

通过 noise - 0.5，调整后的噪声值范围是 [-0.5, 0.5)，再乘以 0.2 后范围是 [-0.1, 0.1)。这使得对颜色的调整是有正有负的，部分像素的亮度会增加，部分会减少，整体上避免了颜色偏白的现象。

这样就好多了，我们还可以给 random 函数加上 iTime 参数，让噪点运动起来！

float noise=random(uv+iTime);

但是有一个问题，因为我演示代码基本上都是用的 vscode 的 shader toy 工具，但是和浏览器对于精度的控制是不一样的，所以如果你在跟随我的代码进行编写的时候发现效果有差异，是正常的。

这是 shader toy 的浏览效果：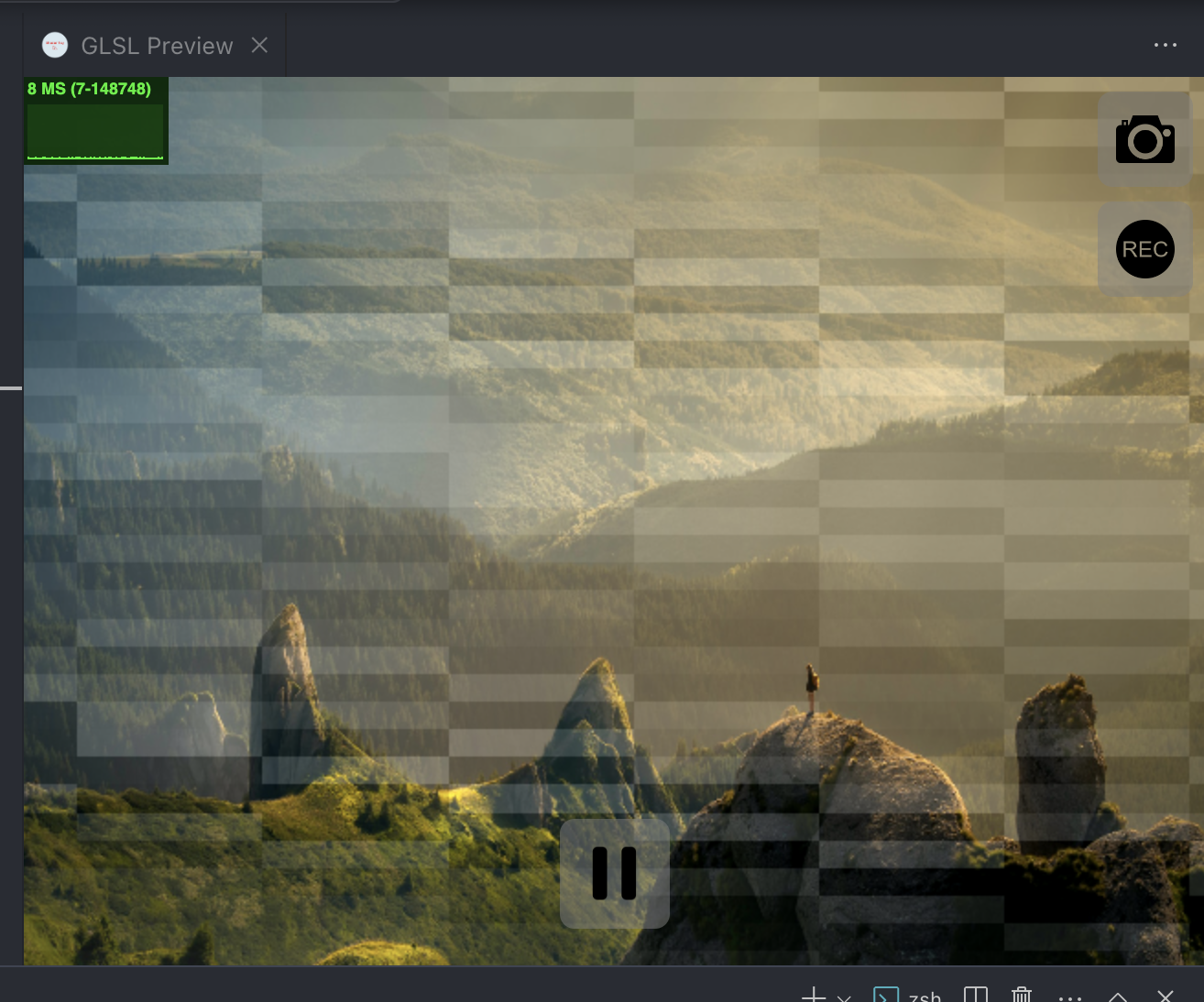

这是网页上的浏览效果：

噪声

噪声也是实现“随机”的一种手段，只不过它能使实现的效果更加偏向“自然”一些。

平时我们在生活中看到的云雾、岩石、火焰等，都有噪声的存在。

到这篇文章编写的时间为止，跟缺少内置的随机函数一样，GLSL 里同样也没有内置的噪声函数。但是在 GitHub 上，也已经有人封装好了一些常用的噪声函数——glsl-noise。我们选择其中比较常用的柏林噪声（Perlin Noise）的 3D 版本，看看它是什么样的。

//
// GLSL textureless classic 3D noise "cnoise",
// with an RSL-style periodic variant "pnoise".
// Author:  Stefan Gustavson (stefan.gustavson@liu.se)
// Version: 2011-10-11
//
// Many thanks to Ian McEwan of Ashima Arts for the
// ideas for permutation and gradient selection.
//
// Copyright (c) 2011 Stefan Gustavson. All rights reserved.
// Distributed under the MIT license. See LICENSE file.
// https://github.com/ashima/webgl-noise
//

vec3 mod289(vec3 x)
{
    return x-floor(x*(1./289.))*289.;
}

vec4 mod289(vec4 x)
{
    return x-floor(x*(1./289.))*289.;
}

vec4 permute(vec4 x)
{
    return mod289(((x*34.)+1.)*x);
}

vec4 taylorInvSqrt(vec4 r)
{
    return 1.79284291400159-.85373472095314*r;
}

vec3 fade(vec3 t){
    return t*t*t*(t*(t*6.-15.)+10.);
}

// Classic Perlin noise
float cnoise(vec3 P)
{
    vec3 Pi0=floor(P);// Integer part for indexing
    vec3 Pi1=Pi0+vec3(1.);// Integer part + 1
    Pi0=mod289(Pi0);
    Pi1=mod289(Pi1);
    vec3 Pf0=fract(P);// Fractional part for interpolation
    vec3 Pf1=Pf0-vec3(1.);// Fractional part - 1.0
    vec4 ix=vec4(Pi0.x,Pi1.x,Pi0.x,Pi1.x);
    vec4 iy=vec4(Pi0.yy,Pi1.yy);
    vec4 iz0=Pi0.zzzz;
    vec4 iz1=Pi1.zzzz;

    vec4 ixy=permute(permute(ix)+iy);
    vec4 ixy0=permute(ixy+iz0);
    vec4 ixy1=permute(ixy+iz1);

    vec4 gx0=ixy0*(1./7.);
    vec4 gy0=fract(floor(gx0)*(1./7.))-.5;
    gx0=fract(gx0);
    vec4 gz0=vec4(.5)-abs(gx0)-abs(gy0);
    vec4 sz0=step(gz0,vec4(0.));
    gx0-=sz0*(step(0.,gx0)-.5);
    gy0-=sz0*(step(0.,gy0)-.5);

    vec4 gx1=ixy1*(1./7.);
    vec4 gy1=fract(floor(gx1)*(1./7.))-.5;
    gx1=fract(gx1);
    vec4 gz1=vec4(.5)-abs(gx1)-abs(gy1);
    vec4 sz1=step(gz1,vec4(0.));
    gx1-=sz1*(step(0.,gx1)-.5);
    gy1-=sz1*(step(0.,gy1)-.5);

    vec3 g000=vec3(gx0.x,gy0.x,gz0.x);
    vec3 g100=vec3(gx0.y,gy0.y,gz0.y);
    vec3 g010=vec3(gx0.z,gy0.z,gz0.z);
    vec3 g110=vec3(gx0.w,gy0.w,gz0.w);
    vec3 g001=vec3(gx1.x,gy1.x,gz1.x);
    vec3 g101=vec3(gx1.y,gy1.y,gz1.y);
    vec3 g011=vec3(gx1.z,gy1.z,gz1.z);
    vec3 g111=vec3(gx1.w,gy1.w,gz1.w);

    vec4 norm0=taylorInvSqrt(vec4(dot(g000,g000),dot(g010,g010),dot(g100,g100),dot(g110,g110)));
    g000*=norm0.x;
    g010*=norm0.y;
    g100*=norm0.z;
    g110*=norm0.w;
    vec4 norm1=taylorInvSqrt(vec4(dot(g001,g001),dot(g011,g011),dot(g101,g101),dot(g111,g111)));
    g001*=norm1.x;
    g011*=norm1.y;
    g101*=norm1.z;
    g111*=norm1.w;

    float n000=dot(g000,Pf0);
    float n100=dot(g100,vec3(Pf1.x,Pf0.yz));
    float n010=dot(g010,vec3(Pf0.x,Pf1.y,Pf0.z));
    float n110=dot(g110,vec3(Pf1.xy,Pf0.z));
    float n001=dot(g001,vec3(Pf0.xy,Pf1.z));
    float n101=dot(g101,vec3(Pf1.x,Pf0.y,Pf1.z));
    float n011=dot(g011,vec3(Pf0.x,Pf1.yz));
    float n111=dot(g111,Pf1);

    vec3 fade_xyz=fade(Pf0);
    vec4 n_z=mix(vec4(n000,n100,n010,n110),vec4(n001,n101,n011,n111),fade_xyz.z);
    vec2 n_yz=mix(n_z.xy,n_z.zw,fade_xyz.y);
    float n_xyz=mix(n_yz.x,n_yz.y,fade_xyz.x);
    return 2.2*n_xyz;
}

代码有点长，但只要会用它就行，给它传入 UV，看看会输出什么？

void mainImage(out vec4 fragColor,in vec2 fragCoord){
    vec2 uv=fragCoord/iResolution.xy;

    float noise=cnoise(vec3(uv,1.));

    vec3 col=vec3(noise);
    fragColor=vec4(col,1.);
}

一团白色，但是有点太大了，我们把 uv 缩放 20 倍，再给三维参数设置为 iTime 看看效果：

float noise=cnoise(vec3(uv*20.,iTime));

有没有一种扭曲黑暗爬行...的感觉？

这就是我们可以明面上看到的噪声的图案了！

噪声转场

上一篇文章里，我们做了遮罩层的转场特效，我们现在可以尝试把噪声叠加到遮罩上。继续引入之前的图案纹理，编写转场函数transition，步骤和之前基本一样，只是我们要给progress加上噪声

vec4 getFromColor(vec2 uv){
    return texture(iChannel0,uv);
}

vec4 getToColor(vec2 uv){
    return texture(iChannel1,uv);
}

float sdCircle(vec2 p,float r)
{
    return length(p)-r;
}

vec4 transition(vec2 uv){
    float progress=iMouse.x/iResolution.x;
    float ratio=iResolution.x/iResolution.y;

    vec2 p=uv;
    p-=.5;
    p.x*=ratio;

    float noise=cnoise(vec3(p*10.,0.));
    float pr=progress+noise*.1;

    float d=sdCircle(p,pr*sqrt(2.4));
    float c=smoothstep(-.1,-.05,d);

    return mix(getFromColor(uv),getToColor(uv),1.-c);
}

void mainImage(out vec4 fragColor,in vec2 fragCoord){
    vec2 uv=fragCoord/iResolution.xy;

    vec4 col=transition(uv);

    fragColor=col;
}

效果图：

这样一来我们的遮罩边缘就变成了噪声的不规则形状，就更加的有那种感觉了

FBM

FBM 全称是Fractal Brownian Motion，意思是“分形布朗运动”，它是将多个具有不同频率和振幅的噪声的结果值相叠加而产生结果的一种随机过程。

它主要被用于构造自然界的云层、山脉、地貌等不规则的形体

（开头的雨林景象用的就是这种技术）。

上面我们用的是柏林噪声，在这里我把噪声换成了更加自然的Simplex噪声，直接从这里拷过来吧。

来实现一下fbm函数：

float fbm(vec3 p){
    // 结果值
    float value=0.;
    // 振幅
    float amplitude=1.;
    // 频率
    float frequency=1.;
    // 空隙率
    float lacunarity=2.;
    // 持久度
    float persistance=.5;
    // 缩放
    float scale=1.;
    // 迭代次数
    int octaves=8;

    for(int i=0;i<octaves;i++){
        float noiseVal=snoise(p*frequency*scale);

        value+=amplitude*noiseVal;
        frequency*=lacunarity;
        amplitude*=persistance;
    }

    return value;
}

咱们这次只需要考虑使用噪音的库，不需要去理解噪音代码的程序原理，简而言之就是先会用，再去研究。我们来仔细解释一下fbm函数：

先定义了几个变量：

• value代表结果值，初始化为 0.0，用于累加每个噪声层的值，最终返回的即为FBM的值。
• amplitude代表了振幅，控制每层噪声对最终值的贡献大小。每次循环中振幅乘以 persistance。
• frequency代表了频率，控制每层噪声的细节密度。每次循环中频率乘以 lacunarity。
• lacunarity代表了空隙率，控制频率的增长速率。通常设为 2，每层噪声的频率增加一倍。
• persistance代表的则是持久度，控制振幅的衰减速率。通常设为 0.5，每层噪声的振幅减半。
• scale就是缩放程度了，控制噪声输入的总体比例。通常设为 1，可以根据具体需求调整。
• octaves代表音度，也就是迭代次数，控制噪声层的数量。更多的层数会产生更复杂和详细的噪声图案。

然后写个 for 循环来叠加噪声，叠加次数就是音度（迭代次数），在叠加的同时升高频率（持续增加细节密度，因为每一次循环都会乘以 2），降低振幅（乘上了持久度，设置的是 0.5，会持续衰减）。

我们来看看实际效果：

void mainImage(out vec4 fragColor,in vec2 fragCoord){
    vec2 uv=fragCoord/iResolution.xy;
    float noise=fbm(vec3(uv,0.));
    vec3 col=vec3(noise);
    fragColor=vec4(col,1.);
}

这种就是像云层一样的噪声图案了。

消融效果

什么是消融效果？举一个简单的例子：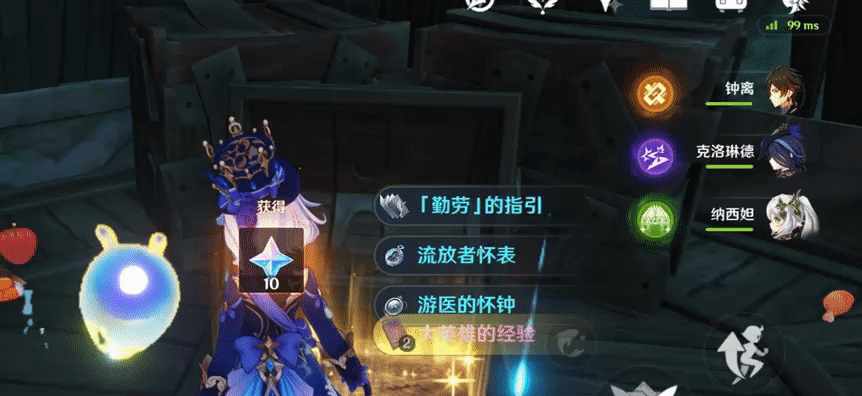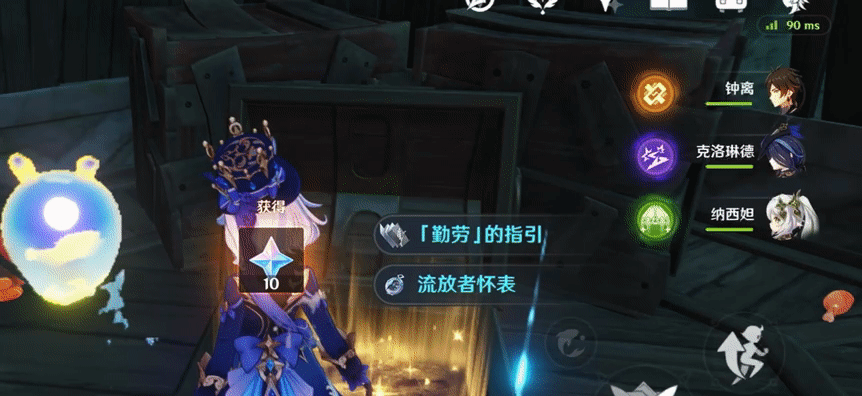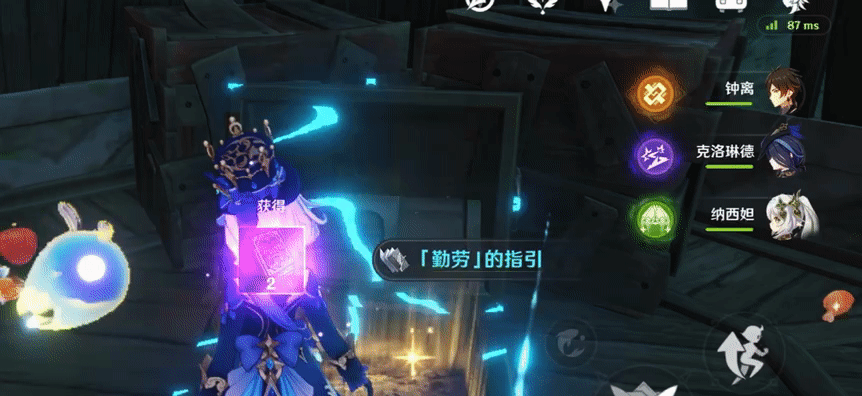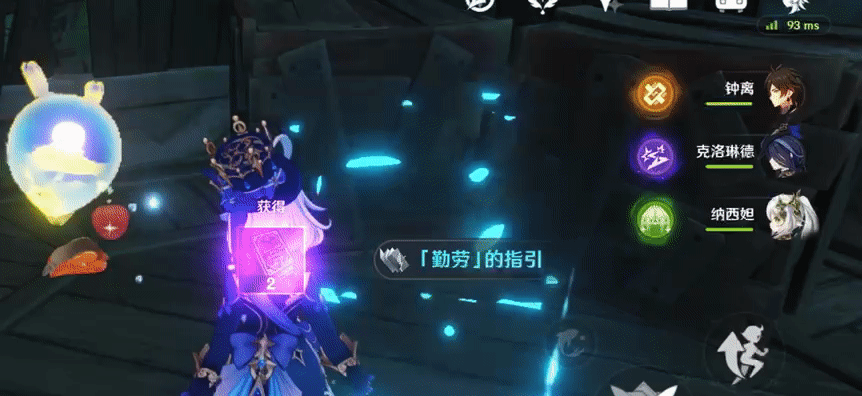

这是游戏《原神》里，玩家开启宝箱之后，宝箱产生的消融效果。

那么，这种消融效果，要怎么实现？刚刚学到的FBM函数就可以做到：
我们保留之前关于FBM函数相关的东西，我们在此之上新建一个dissolve函数，用于实现消融效果：

vec4 getFromColor(vec2 uv){
    return texture(iChannel0,uv);
}

vec4 getToColor(vec2 uv){
    return texture(iChannel1,uv);
}

vec4 dissolve(vec2 uv) {
    float progress = iMouse.x / iResolution.x;
    float ratio = iResolution.x / iResolution.y;

    vec2 p = uv;
    p -= .5;
    p.x *= ratio;
    float noise = fbm(vec3(p, 0.));
    noise = (noise * .5) + .5;
    float pr=smoothstep(progress-.01,progress,noise);
    vec4 col = getFromColor(uv);
    vec4 col1 = getToColor(uv);
    col.rgb=mix(col.rgb,col1.rgb,1.-pr);

    return col;
}

在消融函数里，我们复制了一个二维变量uv给变量p，然后咱们把它居中，并且使用它来创建fbm函数的噪声。

使用smoothstep函数将progress与noise相比较，progress从左侧开始是 0，小于noise的时候，pr会返回一个 1，鼠标往右慢慢移动的时候，porgress会慢慢变大，pr也会慢慢变成小于 1 的值。这里.rgb 的意思是颜色向量的前三个分量，我们不做透明度的处理。

另外，我们的代码里，为了避免鼠标拖到最左侧的时候，已经出现了噪声的问题，我们得让噪声的值域接近[0,1]，引发问题的原因在于值不在 0 和 1 之间变化，fbm生成的值域大概是在[-1, 1]。所以我们对Noise做了处理，乘以.5 之后再加上 .5，使其接近我们需要的值域。

这里运行起来如果有点卡顿的话，可以考虑在 FBM 函数里面把迭代次数参数 octaves 改的小一点，比如改成 2

这是 8 的效果：

这是 2 的效果：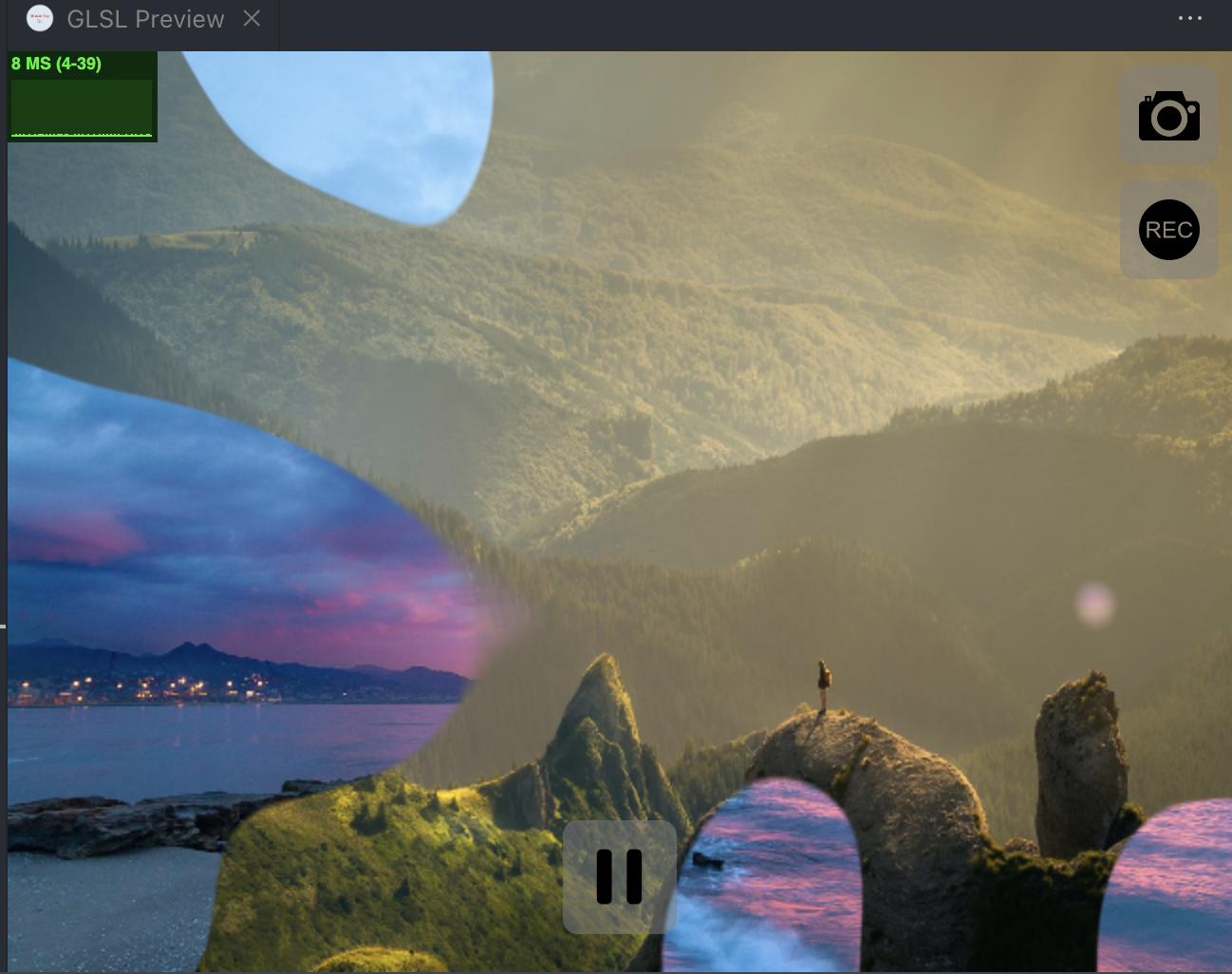

经过上面的调整，我们实际上还是会发现有一点误差，尤其是噪点经过了计算处理之后，所以我们要重新设计一个新的函数来降值的值域映射到新的值域上：

float remap(float a,float b,float c,float d,float t)
{
    return clamp((t-a)/(b-a),0.,1.)*(d-c)+c;
}

我来解释下这个函数的具体作用：
1.(t - a) / (b - a)：
将输入值 t 归一化到 [0, 1] 范围内。假设 t 在 [a, b] 之间，计算得到的值为：

• 当 t = a 时，结果为 0。
• 当 t = b 时，结果为 1。

• 当 a < t < b 时，结果在 0 和 1 之间。

  2.clamp((t - a) / (b - a), 0.0, 1.0)：
  对归一化后的结果进行裁剪，确保其在 [0, 1] 范围内。如果 t 超出了 [a, b] 范围，则结果被裁剪为 0 或 1：

• 当 t < a 时，结果为 0。

• 当 t > b 时，结果为 1。

  3.clamp((t - a) / (b - a), 0.0, 1.0) * (d - c) + c
  将裁剪后的值从 [0, 1] 范围缩放到 [c, d] 范围：

• 当结果为 0 时，输出为 c。
• 当结果为 1 时，输出为 d。
• 当结果在 0 和 1 之间时，输出在 c 和 d 之间线性插值。

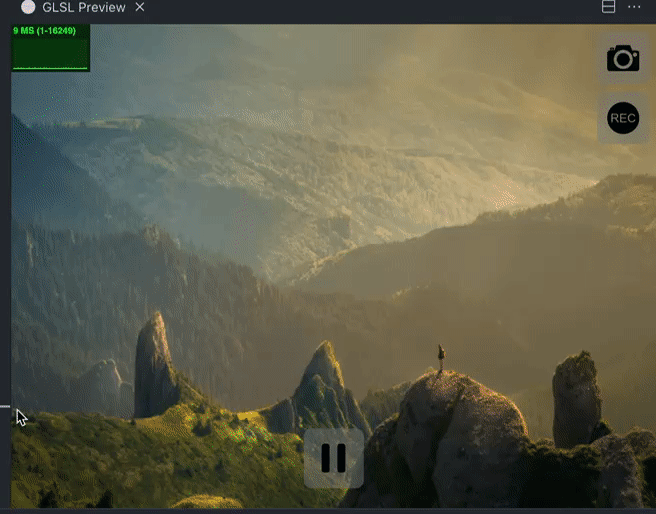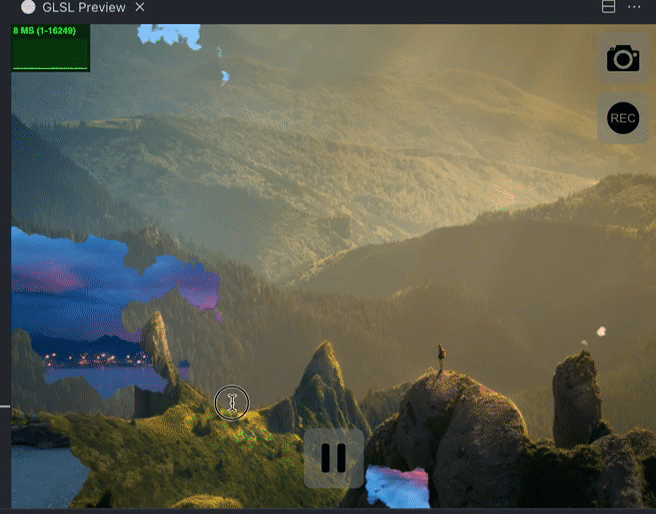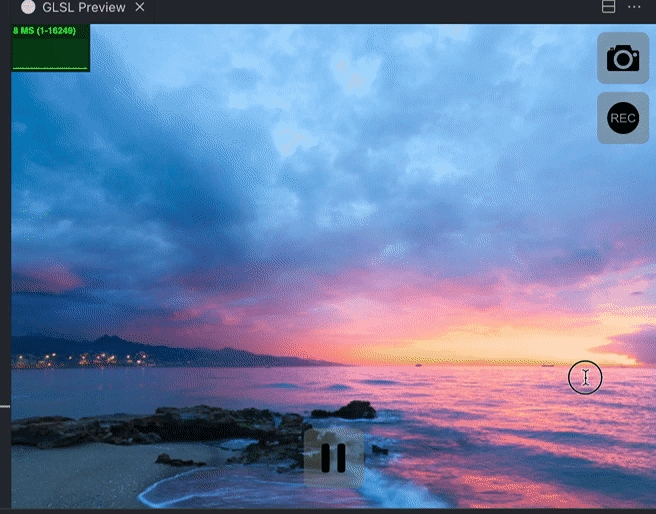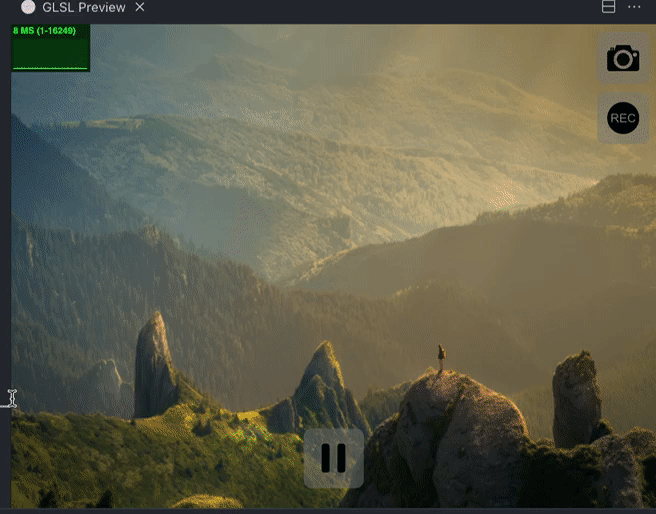
这样一来，我们就实现了一个基本的消融效果。但是在游戏里，可以看到消融的时候，有一圈的亮边，我们来跟着一起也做一下吧

我们接着定义两个变量：亮边的长度和亮边的颜色

    float edgeWidth=.1;
    vec3 edgeColor=vec3(0.3255,0.6824,0.8);

绘制一下亮边的遮罩看看，长度是edgeWidth，混合度就是噪声和位置的差，然后我们把遮罩输出一下看看：

float edge=1.-smoothstep(0.,edgeWidth,noise-progress);
col.rgb=vec3(edge);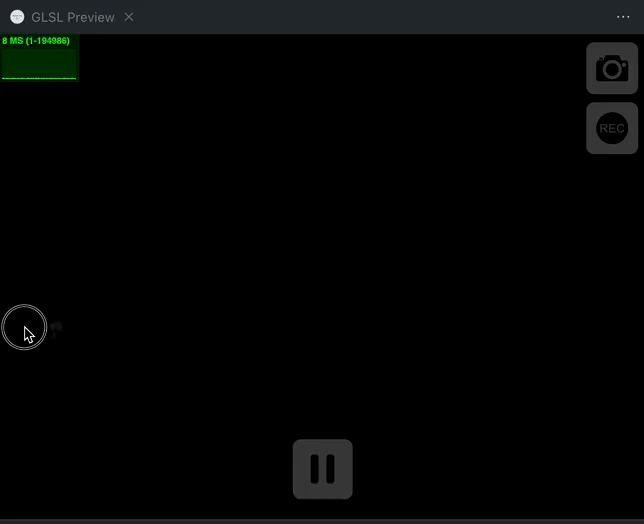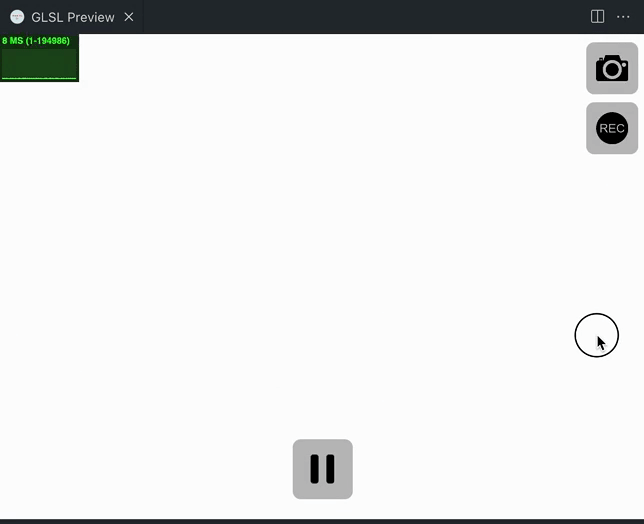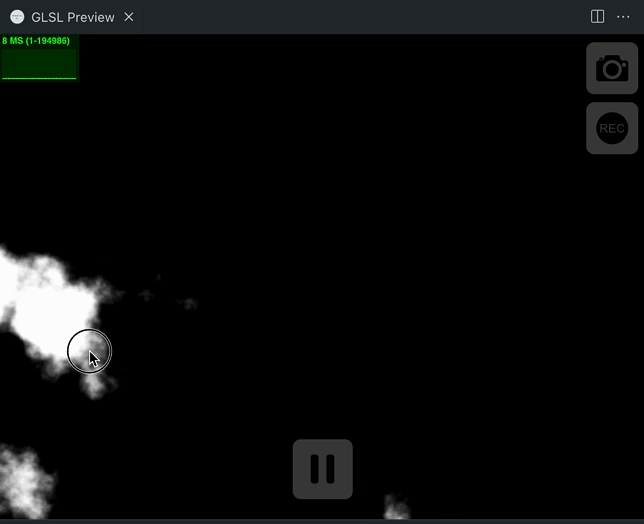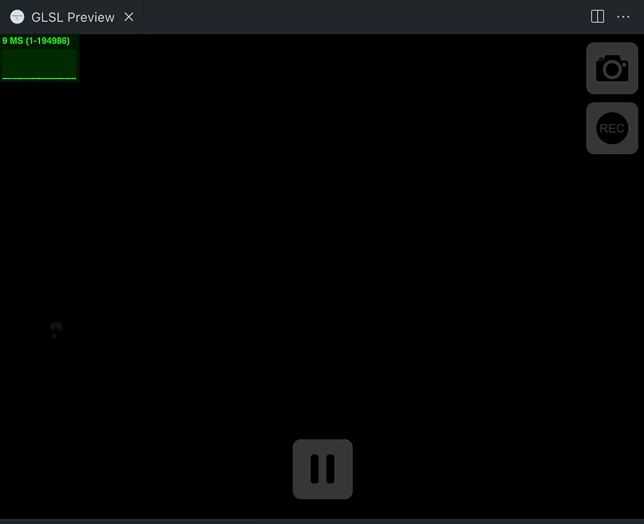

来吧我们来解释一下，根据smoothstep函数的定义，当我们的noise减去progress的值小于 0 的时候，也就是noise小于progress的时候，smoothstep就会返回 0，edge就会返回 1，这个时候呢，鼠标就应该是在画布的右侧，画布整体变成了白色，表示的阶段是消融已经结束；反之，如果相减的值，大于edgeWidth，返回 1，edge返回 0，鼠标在画布的左侧，整体是黑色，也就是表示的消融变化之前；相减的值，在 0 和edgeWidth之间，那就表示处在消融变化之中。

总结之后，我们正式应用一下亮边元素。

// col.rgb=vec3(edge);
col.rgb=mix(col.rgb,edgeColor,1.-pr);

咦，亮边的确是出现了：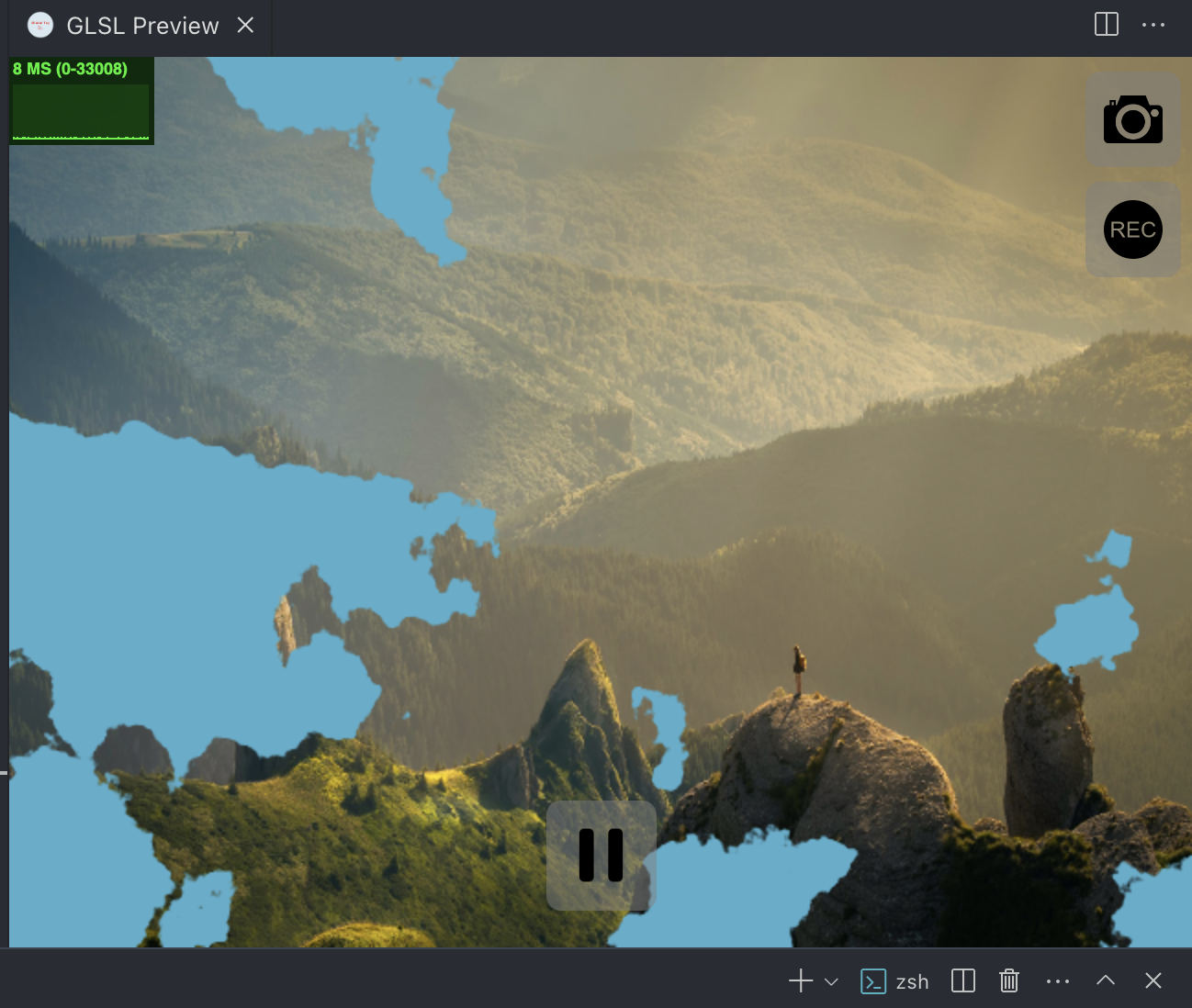

但是，消融部分也跟着消失了，原因在于，消融部分的调用顺序在前，跑到亮边的下面一层去了，加上亮边本身的范围要比消融的范围大，所以被遮盖了。我们重新写一下：

vec4 dissolve(vec2 uv) {
    float progress = iMouse.x / iResolution.x;
    // float progress = sin(iTime);
    float ratio = iResolution.x / iResolution.y;

    vec2 p = uv;
    p -= .5;
    p.x *= ratio;
    float noise = fbm(vec3(p, 0.));
    // noise = (noise * .5) + .5;
    noise = remap(-1., 1., 0., 1., noise);

    vec4 col = getFromColor(uv);
    vec4 col1 = getToColor(uv);


    float edgeWidth=.1;
    vec3 edgeColor=vec3(0.3255,0.6824,0.8);
    float edge=1.-smoothstep(0.,edgeWidth,noise-progress);
    col.rgb=mix(col.rgb,edgeColor,edge);

    float pr=smoothstep(progress-.01,progress,noise);

    col.rgb=mix(col.rgb.rgb,col1.rgb,1.-pr);

    return col;
}

现在的基本是对了，但是，还有个优化点，我们将鼠标拖到最左边。

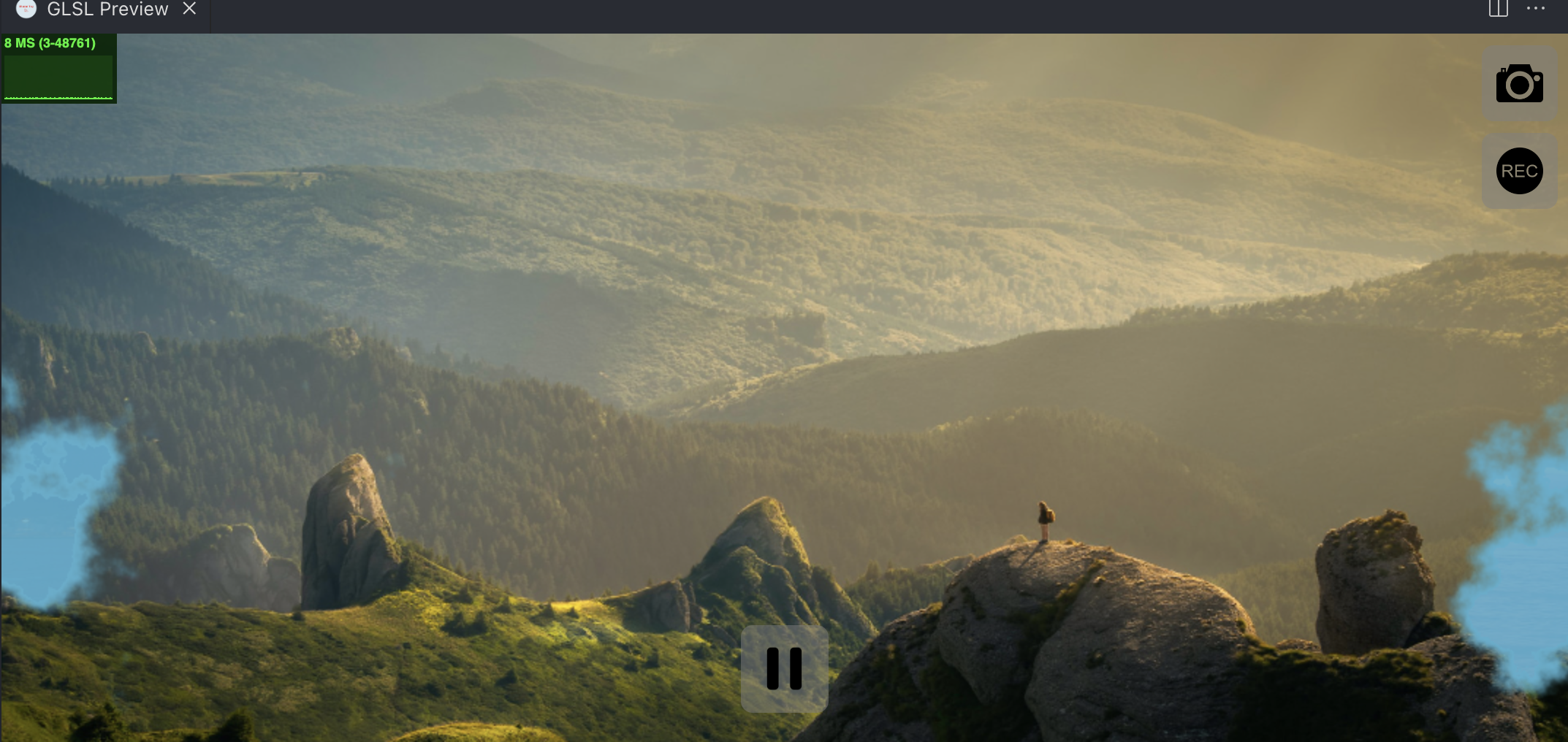
我们发现，左侧不该出现的亮边也出现了，这是因为这个时候的progress是 0，减去的值就是noise，但是，它的值不一定会大于 亮边长度edgeWidth，所以edge不一定等于 0。我们要确保在左侧混合因素的值得是 0 才行。

怎么做？

col.rgb=mix(col.rgb,edgeColor,edge*step(.0001,progress));

咱们给混合因素上一个乘数值，当progress小于一个很小的值（如0.0001）时，这个值会返回 0，否则就返回 1，这样就能确保鼠标位于最左侧时没有多余的亮边出现了。

下面是最终的效果：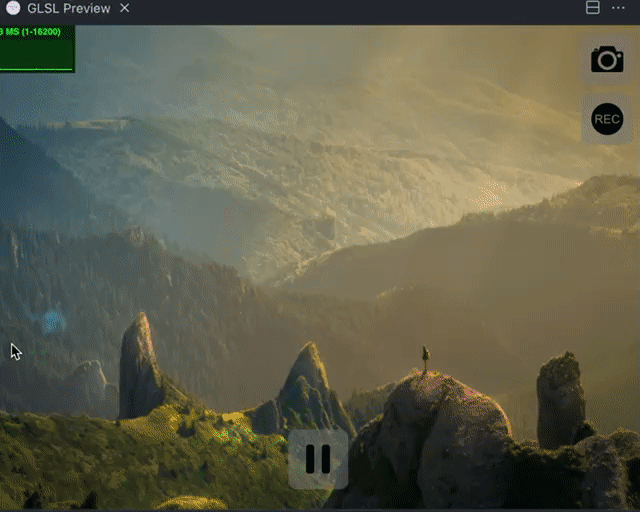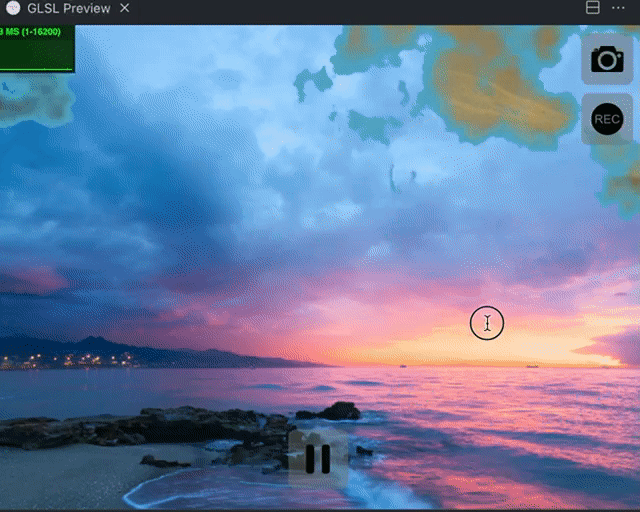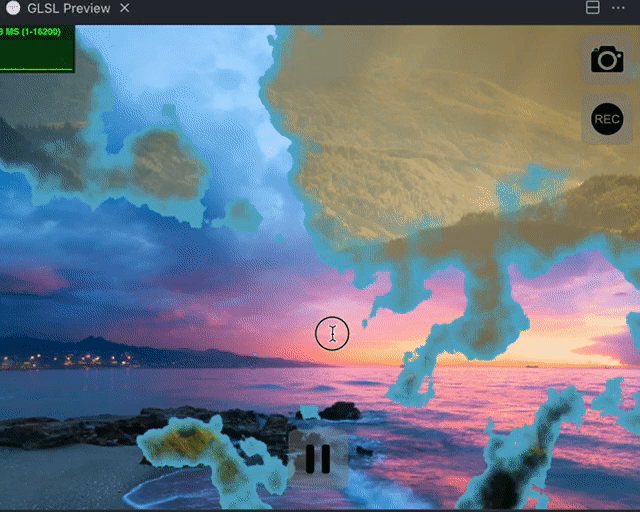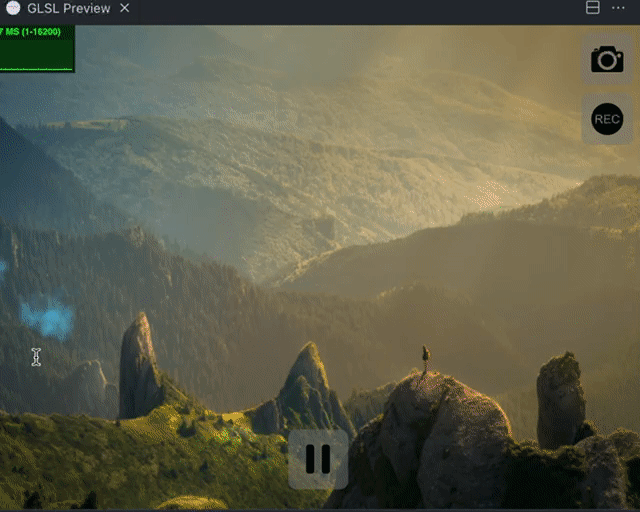

这一篇的内容有点多，我罗列一下主要的点： 1.随机函数random是一种实现“随机”的方法，我们可以通过它得到带有噪点的图形

2.噪声noise也是实现“随机”的方式，得到的结果也是更“自然”。我们可以将噪声叠加到一些规则的图形之上，让他变得不规则。

3.分形布朗运动FBM将多个不同频率，振幅的噪声的结果叠加，产生一种随机的过程，经常用于模拟自然界的山脉等等不规则物体，我们可以使用FBM来实现一种“消融”的效果。

总的来说，“随机”效果，可以为我们的着色器应用添加各种有意思的效果，多加利用吧。