mix函数
到我们现在为止,我们做出的示例图基本都是黑色和白色,非常的单调,那么我该怎么做,才可以给这些图形染上颜色呢?
这就是我们马上要提到的函数,mix的工作了。这是一个GLSL的内部函数。也被称之为混合函数
其实现逻辑很简单,一行代码就可以望到头
#define mix(x,y,t) x*(1.-t)+y*t它接受 3 个参数:前 2 个参数x和y分别对应 2 个值,最后一个参数t代表混合程度,如果t为 0,则值就等于x;如果t为 1,则值就等于y,如果t为 0 到 1 内的值,则值就等于x与y之间逐渐变化的值。
创建渐变色
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uvCenter=(2. * fragCoord - iResolution.xy)/iResolution.y;
vec2 uv = fragCoord / iResolution.xy;
vec3 col1=vec3(1.,0.,0.);
vec3 col2=vec3(0.,1.,0.);
vec3 col=mix(col1,col2,uvCenter.x);
fragColor=vec4(col, 1.);
}我声明了两个uv,一个是居中以及根据画布尺寸做了调整的归一化坐标,另一个是没有处理过的归一化坐标,我们使用了mix方法来指定了两个颜色,红色和绿色,混合程度就是uv的x轴

这样一来,我们就得到了一个沿着x轴渐变的颜色
给图形染色
mix可以给图形染色特定的颜色。
前文中,我们聊到了SDF函数,在一个形状的外部,他的值为整数,在内部,就是负数。根据这个特性,我们可以定义两个颜色值,一个是Inner一个是Outer,分别代表了形状内部和外部的颜色,我们再使用mix函数将他们混合起来,混合程度就用SDF函数平滑之后的效果
float sdBox( in vec2 p, in vec2 b ) {
vec2 d = abs(p)-b;
return length(max(d,0.0)) + min(max(d.x,d.y),0.0);
}
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uv =(2. * fragCoord - iResolution.xy)/iResolution.y;
float d = sdBox(uv, vec2(.6, .3));
float c = smoothstep(0., .002, d);
vec3 colInner = vec3(1., 0., 0.);
vec3 colOuter = vec3(1., 1., 1.);
vec3 col = mix(colInner, colOuter, c);
fragColor = vec4(col, 1.);
}

这里解释一下为什么要把平滑处理之后的结果作为混合程度:
smoothstep(0., .002, d)生成了一个从0到1平滑过渡的值,具体来说:
当d接近0时,c接近0,这表示该点非常接近或在矩形内部。
当d接近0.002时,c接近1,这表示该点接近矩形边缘。
这样做的目的是为了在矩形的边缘创建一个平滑的过渡效果,而不是产生一个硬边。这使得颜色从内部的红色(colInner)平滑过渡到外部的白色(colOuter)。smoothstep的平滑过渡效果避免了颜色的突然变化,生成视觉上更为柔和和自然的边缘。
通过这种方式,c的值平滑地从0变到1,从而使mix(colInner, colOuter, c)能够创建一个从红色到白色的平滑过渡,而不是一个硬边界。这种方法通常用于反走样,以减少边缘的锯齿效应。
形状转变效果
mix函数不仅可以混合颜色,还可以混合别的东西,比如说形状,只要是维度相同的两个值,都可以拿来混合。
比方说我现在创建两个SDF图形,长方形和圆形,把其形状通过mix混合起来,混合程度参数就用iTime。外部包裹了两层函数:
1.sin函数负责周期性的变化
2.abs函数负责确保混合程度的值是正数的

OK,我们得到了一个随着时间流逝,在圆和长方形之间反复变化的图形
重复图案
之前都是单个图形进行绘制,实际上在UV变化那部分的讲解时,我们已经尝试过使用fract函数来实现“重复”的操作了,利用这一点,我们可以创建出其他的常见的重复图案。这个函数的原理是取小数点。
条纹
我们可以先用step函数绘制出一根线条(其实就是靠右边的一块颜色块儿)
再使用fract函数来重复UV,注意这一步要写在绘制线条之前。
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uv = fragCoord / iResolution.xy;
uv = fract(uv * 16.0);
vec3 c = vec3(step(.5, uv.x));
fragColor = vec4(c, 1.0);
}
这里要格外注意fract的使用规则,注意事项我已经更新到上一篇文档的重复部分了。
使用居中且自适应画布的uv,不太推荐使用fract,因为它会导致坐标折叠回0到1的范围,产生不可预期的图案或重复图案。特别是当uv包含负数时,fract会将这些负数转化为正数的小数部分,从而导致图案变得复杂和混乱。
波浪
把刚刚的条纹改成y轴方向,然后对uv的y轴进行修改,加上x的sin值,这会导致什么情况呢?
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uvCenter = (2.0 * fragCoord - iResolution.xy) / iResolution.y;
vec2 uv = fragCoord / iResolution.xy;
uv.y += sin(uv.x);
uv = fract(uv * 16.);
vec3 c = vec3(step(.5, uv.y));
fragColor = vec4(c, 1.0);
}
视觉上已经有点弯曲了,但是不够明显,我们对sin函数做一下微调,比如对x乘以5,之后对sin的整体值微调一点比如.2
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uvCenter = (2.0 * fragCoord - iResolution.xy) / iResolution.y;
vec2 uv = fragCoord / iResolution.xy;
uv.y += sin(uv.x * 5.) * .2;
uv = fract(uv * 16.);
vec3 c = vec3(step(.5, uv.y));
fragColor = vec4(c, 1.0);
}现在就非常的合适了:
网格
网格实际上就可以看成是2个互相垂直的条纹叠加形成的形状
首先我们用fract来重复uv,然后再用我们之前学到的并集来处理x轴和y轴,将他们合并起来。另外,为了解决画布的长宽不相等的问题,我们还要处理一下比例。
整体代码如下
float opUion(float d1, float d2) {
return min(d1, d2);
}
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uvCenter = (2.0 * fragCoord - iResolution.xy) / iResolution.y;
vec2 uv = fragCoord / iResolution.xy;
uv.x*=iResolution.x/iResolution.y;
uv = fract(uv * 16.);
vec3 c = vec3(opUion(
step(.25, uv.x),
step(.25, uv.y))
);
fragColor = vec4(c, 1.0);
}
波纹
要注意,除了fract函数,sin也是有重复特性的,初中数学吧,这样一来我们就不需要用fract函数了,用sin来重复SDF函数的距离
float opUion(float d1, float d2) {
return min(d1, d2);
}
float sdCircle (vec2 p, float r) {
return length(p) - r;
}
void mainImage(out vec4 fragColor,in vec2 fragCoord){
vec2 uvCenter = (2.0 * fragCoord - iResolution.xy) / iResolution.y;
float circleVal = sdCircle(uvCenter, .5);
circleVal = sin(circleVal * 40.);
float circle = smoothstep(0., .02, circleVal);
fragColor = vec4(vec3(circleVal), 1.0);
}
极坐标
我们到目前为止,涉及到的Shader的默认坐标系是直接坐标系,除了这一类坐标系,还有一个坐标系,叫做极坐标系,这个坐标系可以画出一系列基于圆形的图案出来

如果上面这个示意图,极坐标系是由两个维度构成的,极角φ和半径r。
先将uv进行居中处理,图中的极角φ可以通过atan函数计算直角坐标系的反正切值就能算出来了。第二个维度半径r,则用length函数计算直角坐标系到原地的距离就可以轻松算出。所以,我们来整一个比较具现化的极坐标展示吧:
vec2 cart2polar (in vec2 uv) {
float phi = atan(uv.y, uv.x);
float r = length(uv);
return vec2(phi, r);
}
void mainImage (out vec4 fragColor, in vec2 fragCoord) {
vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;
uv = cart2polar(uv);
fragColor = vec4((uv), 0, 1.0);
}这样出来的就是这张图: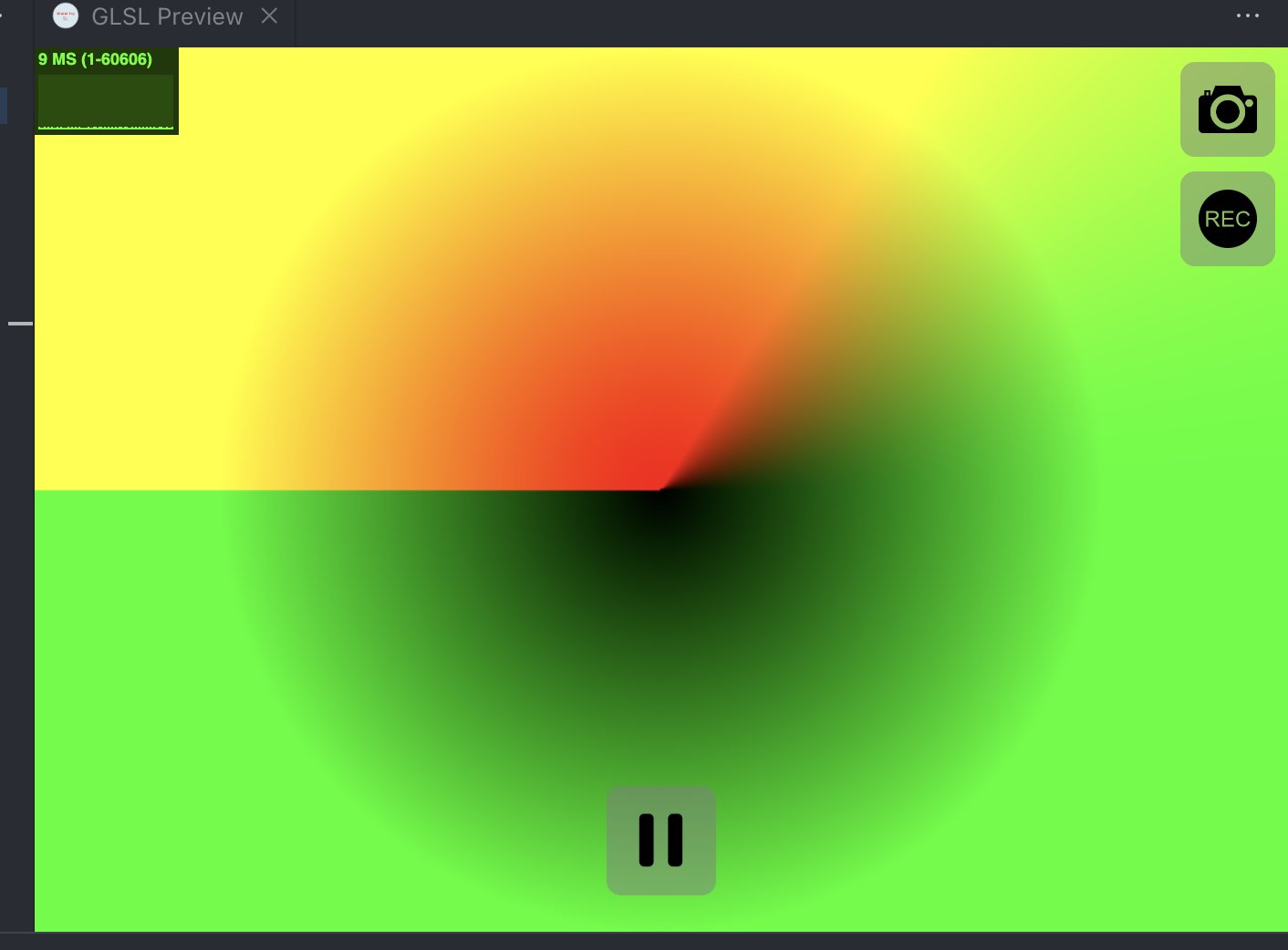
我们可以继续使用极坐标搭配其他的函数,比如sin来画出各种各样的形状
放射形
直接用sin
vec2 cart2polar (in vec2 uv) {
float phi = atan(uv.y, uv.x);
float r = length(uv);
return vec2(phi, r);
}
void mainImage (out vec4 fragColor, in vec2 fragCoord) {
vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;
uv = cart2polar(uv);
float c = step(.0,sin(uv.x * 12.));
fragColor = vec4(vec3(c), 1.0);
}
讲解一下原理吧:我们把uv转换为了极坐标,phi是我们从X轴正方向到点的连线之间的角度(极角),r是点到原点的距离.对极角 phi 进行了正弦函数计算,并乘以一个因子 12。由于 phi 是角度,sin(uv.x * 12.0) 将在每个极角周期内重复 12 次。这意味着每隔 π/6(30 度)就会重复一次正弦波的周期,这导致图案中每 30 度出现一次明暗变化。
正弦函数 sin(x) 在 [0,2?] 范围内有一个完整的周期,并且在每个周期内从 -1 变化到 1 再回到 -1。这个周期性的波形导致了图像中明暗交替的效果。
所以说,[0,1]这个范围是明亮,[-1,0]这个范围是暗淡。
注意:在 GLSL 中,颜色分量的范围通常在 [0, 1] 之间。如果 c 是负值,那么 vec3(c) 的分量将被截断为 0(黑色)。如果 c 是正值但小于 1,那么颜色将是灰色到白色的渐变。所以我们为了避免这种渐变,就用到了阶梯函数来做
螺旋形
也是用sin函数,但是参数要更改,是半径乘以倍数 + 角度,乘以半径是因为要随着半径的增加,使其sin函数在半径方向上进行快速变化。当角度变化时,每个固定的 ?对应的角度值 ? 会在 [0,2?] 之间循环变化。这意味着正弦波的相位不仅随? 变化,还会随 ? 变化,形成一个螺旋状的图案。
vec2 cart2polar (in vec2 uv) {
float phi = atan(uv.y, uv.x);
float r = length(uv);
return vec2(phi, r);
}
void mainImage (out vec4 fragColor, in vec2 fragCoord) {
vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;
uv = cart2polar(uv);
float c = step(.0,sin(uv.y * 20. + uv.x));
fragColor = vec4(vec3(c), 1.0);
}