UV坐标

这是主体代码：

void mainImage(out vec4 fragColor,in vec2 fragCoord){
}

前面我们已经直到了，这个是主体函数mainImage，里面有两个参数，一个是四维变量 fragColor，代表输
颜色、fragCoord代表输入坐标，并且我们还有一个内置的变量iResolution代表着画布的大小。

在Shader中，一个变量的基本值都是分布在[0. , 1.]之间的，也就是：

在图形处理中，归一化 UV 坐标将每个轴的坐标限制在 0 到 1 之间。这是大多数图形API和硬件期望的纹理坐标范围。

而现在的输入坐标的值远远地超过了它，我们也就需要将它给“归一化”。

UV坐标的解释

  • U坐标：通常对应的是纹理的水平方向，对应的是传统的X轴
  • V坐标：通常对应的是纹理的竖直方向，对应的是传统的Y轴

在处理纹理时，归一化的坐标系统让你能够独立于纹理的实际像素尺寸，统一处理纹理坐标。例如，无论纹理的实际尺寸是 256x256 像素还是 1024x1024 像素，UV坐标 (0.5, 0.5) 总是指向纹理的中心点。

用输入坐标fragCoord除以画布大小iResolution.xy，我们就能得到一个归一化的坐标，把它命名为uv。

    vec2 uv = fragCood / iResolution.xy;

来看一下x轴坐标分布情况：

现在我们代码里第三个值是0，我们暂时只看前两个，可以看到x坐标从左边开始是黑色，值是(0, 0)，在最右边是红色，值是(1,0)，中间则是分布在(0, 1)之间的值。从整体上来看，我们得到的是一个从左到右渐变的图案。

一样的，我们再来看一下y坐标的分布：

可以看到y坐标从底下开始是黑色，值是(0,0)，到最上面是纯绿色，值是(0,1)，而中间则是分布在(0,1)之间的值。从整体上看，我们得到了一个纵向的渐变图案。

接下来，我们同时输出x坐标和y坐标的分布：
直接传递一个vec2作为vec4的第一个参数，剩下只需要两个参数位置了：

左下角原点是黑色，值是(0,0)，右下角是红色，值是(1,0)，左上角是绿色，值是(0,1)，右上角是黄色，值是(1,1)，中间的所有值在(0,0)到(1,1)这 2 个区间分布。从整体上看，我们得到了一个有多种颜色的渐变图案。

这就是所谓的UV坐标，它代表了图像（这里指画布）上所有像素的归一化后的坐标位置，其中U代表水平方向，V代表垂直方向。

图形的绘制

图形界最常见的东西，就是圆。
说一下设计思路：

先计算uv坐标上的点到原点的距离，这个可以使用GLSL自带的方法length来实现

length 函数返回一个向量的长度（模），它是一个标量（即一个实数），始终为非负数。这个长度是向量从原点到指定点的距离，因此总是正数或零。会计算 uv 向量从原点 (0, 0) 到指定点 (uv.x, uv.y) 的距离，这个距离总是非负的。

    float d = length(uv);
    fragColor = vec4(vec3(d), 1.0);

实现效果是这样的：

左下角是黑色的原点，值是(0,0)，从原点向右上方向辐射的径向渐变，上面每个点的值代表的就是该点到原点的距离，越靠近原点距离越小，越接近黑色，反之越远离原点距离越大，越接近白色。

我们怎么把这个玩意儿挪到中间呢？前面说了，坐标是在(0,0)到(1,1)这个区间分布的，那么要居中的话，我们可以让区间扩大到(-1,-1)到(1,1)。这样会发生什么？

那就是(0,0)这个原点会出现在屏幕的正中间

（注意这一行代码要放在length函数代码的上面。）

于是我们有了：

怎么样，是不是有那种味儿了？原点黑色在中央位置，发散到四面八方，越远颜色越接近白色

但是目前好像并不是完好的圆形，我们稍微把preview的窗口拉小一点：

这就是一个椭圆了，这是什么问题？

因为，uv坐标的值并不会去自动适应画布的大小，我们该怎么做呢？

我们需要计算画布的比例，将画布长除以画布宽就能算出，再将UV的x坐标与比例相乘即可。

就是这句关键的语句：

    uv.x *= iResolution.x / iResolution.y;

调整 uv.x 可以确保纹理在不同分辨率的画布上保持正确的比例，而 uv.y 不需要调整，因为它已经在 [0.0, 1.0] 的范围内且不受画布宽高比变化的影响。

那么我们整理一下：
UV的最终合理的表达式是：

    vec2 uv = (fragCoord / iResolution.xy) * 2. - 1.;
    uv.x *= iResolution.x / iResolution.y;

我们可以把它简化为：

    vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;

这是怎么计算出来的？
首先，我们将 uv.x 调整宽高比：

uv.x = ((fragCoord.x / iResolution.x) * 2.0 - 1.0) * (iResolution.x / iResolution.y);

同时 uv.y保持不变：

uv.y = (fragCoord.y / iResolution.y) * 2.0 - 1.0;

再给uv.y合并一下：

uv.y = (2.0 * fragCoord.y - iResoluation.y) / iResolution.y

对于uv.x：
我们合并之后得到

uv.x = (2.0 * fragCoord.x / iResolution.x - 1.0) * (iResolution.x / iResolution.y);

进一步化简：

uv.x = (2.0 * fragCoord.x * (iResolution.x / iResolution.y) / iResolution.x - (iResolution.x / iResolution.y));
uv.x = (2.0 * fragCoord.x / iResolution.y - iResolution.x / iResolution.y);
uv.x = (2.0 * fragCoord.x - iResolution.x) / iResolution.y;

综合所得：
uv.x 和 uv.y合并之后就是：

vec2 uv = (2.0*fragCoord-iResolution.xy)/iResolution.y;

OK，到目前为止，我们得到了一个完整的圆形径向渐变，但我们要的并不是渐变，而是实实在在的圆形。

首先我们可以进行思考：
这个朦胧的渐变圆的原理是 纯黑色的点在(0,0)，处于画布中间，其他部分的向周围辐射的点的值都是大于0的，都非纯黑色

那么目标就自然而然的来到了把周边的点的值都变成0。

这里就要补充一个小知识了：
在Shader中，值的显示范围只会是[0,1]之间，也就是说，小于 0 的负数实际显示的值还是 0（黑色），大于 1 的数实际显示的值还是 1（白色）。我们可以利用这一点，给距离d减去一个值（这里我取了 0.5），制造出一片负数的区域，而这片区域不就是我们所要的黑色吗？（注意这一行代码要写在length函数的下面。）

接下来我们只需要把周边模糊的部分去除，就是我们想要的圆形了，我们可以使用if判断逻辑来进行：

我们先定义一个中间变量c，用if语句来判断距离d的大小，如果大于 0，代表的是除了中间纯黑区域外的渐变区域，将它们的值设为 1（白色）；反之，就代表的是中间的纯黑区域，将它们的值设为 0（黑色），最后将中间变量直接作为结果输出即可。

因为d是在上面减去过0.5的，其实就是相当于判断，是否处于半径为0.5的圆的里面，因为画布全长为-1到1（上面UV居中之后的范围就是这样的），所以圆的半径占了四分之一个画布，也就是全长直径占了半个画布。

然而，在Shader的编写中，我们应当尽量避免使用if语句，为什么呢？因为GPU是并行处理结果的，而if语句会让处理器进行分支切换这一操作，处理多个分支会降低并行处理的性能。那么如何优化掉if语句呢？我们可以用GLSL其中的一个内置函数来代替它。

这个内置函数是 step函数，也被称作“阶梯函数”，是因为它的图像是阶梯的形状，如下图所示：

它是一个矢量化的操作，所有的计算都可以在同一条指令下进行，避免了线程分歧和性能损失。相比之下，if-else 会引入分支切换，每个分支可能需要不同的指令路径，导致处理器无法高效利用并行计算的优势。

代码的表现形式是这样的：

step(edge,x)

它接受 2 个参数：边界值edge和目标值x，如果目标值x大于边界值edge，则返回 1，反之返回 0。

用它来替换掉我们刚刚使用的if else：

这一步，不仅简化了代码，还优化了shader的性能

但是，如果仔细观察的话，我们生成的圆还是很有问题的，毕竟有锯齿，影响美观。

那我们就再来认识个GLSL函数：smoothstep函数，它也被称作“平滑阶梯函数”，是因为它的函数图像是一个平滑过的阶梯的形状，如下图所示：

代码的表现形式是：

smoothstep(edge1,edge2,x)

比起step阶梯函数多了一个参数，我们可以将它的边界值定为edge1和edge2：如果目标值x小于边界值edge1，则返回 0；如果目标值x大于边界值edge2，则返回 1；如果目标值x在 2 个边界值之间，则返回从 0 到 1 平滑过渡的值。

这样一来就圆滑很多了。

图形效果

虽然上面我们使用Shader画出一个圆的操作比传统的办法要繁琐一点，但是，重点是shader能够带来的可能性，比如实现一些特殊的效果

模糊效果

我们为了保持圆滑，使用了smoothstep方法来进行了绘制图形，第二个参数就是我们用到了很小的参数.01，现在我们把它放大一点：

能够看到非常明显的边缘模糊效果。

随着渐变区域的扩大，圆形的边缘变得模糊了起来，这是因为两个边界值的差变大了，渐变的区域也就随着变大了，这样就营造出了一种模糊的效果。这种效果实用性非常之高

发光效果

我们这次就不用smooth了，我们直接取倒数，然后乘以一个比较小的值，比如.25

我们就得到了一个看起来很炫酷的发光小球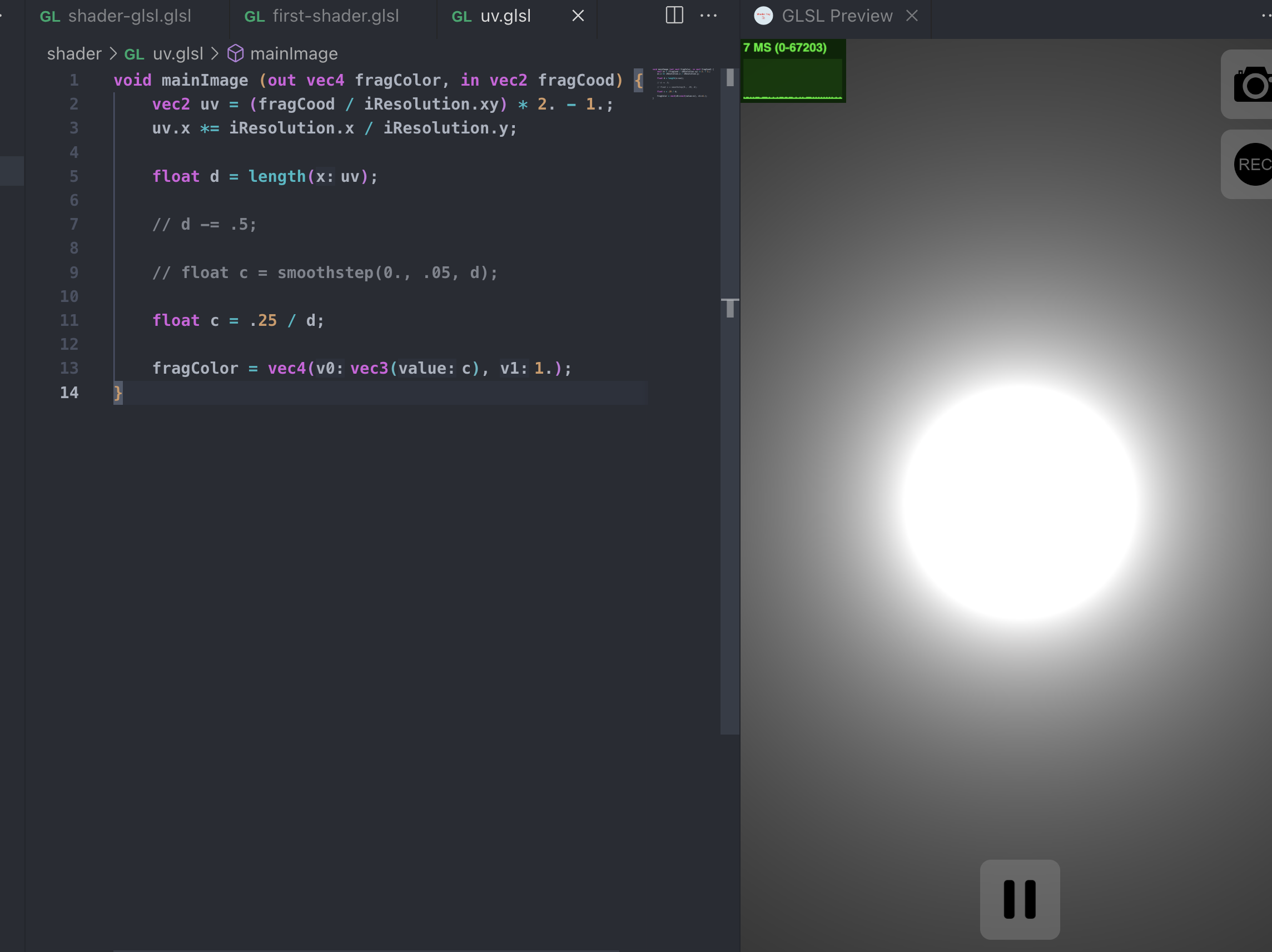

一行简单的代码，但是它实际上是怎么形成的呢？

这是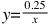的函数分布图，我们的值是(0., 1.)，所以在这段范围内，如果输入的值是(0., .25)那么，输出值都是大于1的，Shader里，输出比1大的都是白色，因此我们能看到中间的白色圆形部分; 当输入值处于(.25, 1.)的区间时，值都是逐渐减小的，比1小，因此会出现渐变的效果。

现在这个图的光的辐射效果有点太强了，我们引入一个内置函数来让他缩小一些

pow函数，它用来计算数字的指数幂，比如说pow(2.0, 3.0)算的就是2的三次方，也就是8，也就是说这个pow函数能让数值指数增长，小数点也是一样可以的。

我们给刚刚的代码加一个pow，指数取1.6

亮度低一点了。

来看一下函数分布图：

函数的走向要比之前往下“躺”一点点了。也就是说输出值整体会低一点，这样的话光的辐射也会低一点。

这样的发光效果换成别的绘图方式可能会很难实现吧，而Shader只要借助数学计算，就能轻松实现

知道Shader的厉害之处后，让我们依旧回到那个最基本的圆形，开始绘制其他图形

SDF函数

圆形，只不过是众多几何图形里的一种，我们同样可用其他的办法画出其他的几何图形。

回顾我们画圆形的时候，所使用的方法

    float d = length(uv);
    d -= .5;

其实我们可以把它抽象为一个函数，名字叫做sdCircle

float sdCicrle (vec2 p, float r) {
    return length(p) - r;
}

void mainImage (out vec4 fragColor, in vec2 fragCoord) {
    vec2 uv = (2. * fragCoord - iResolution.xy) / iResolution.y;

    float d = sdCicrle(uv, .5);

    float c = smoothstep(0., .05, d);
    
    ...
}

这其实最后的调用结果和我们之前写的代码是一模一样的，但是它有一个特殊的含义，那就是这是一个SDF函数

SDF函数，中文译作符号距离函数，SDF 函数通常接受一个点作为输入，并返回该点到几何形状的最近距离。如果该点位于形状内部，距离是负数；如果在形状外部，距离是正数；如果在形状上，则距离是零。这种有符号的距离使得 SDF 函数可以非常灵活地描述各种复杂的几何形状，包括曲面、体积等。

举个例子，这是圆形SDF的数据分布图

图形学大咖 Inigo Quilez把基本上常用的2D图形的SDF函数都列了出来，我在这里贴出来，可以收藏以防备用。直达链接

知道了SDF的概念之后，我们就可以轻松的画出来其他的图形，比如我想要一个长方形，我只需要调用长方形的SDF函数，获取距离之后，使用step或者smoothstep勾画出图形就行

最后修改：2024 年 08 月 14 日
© 允许规范转载
收款不要了，给孩子补充点点赞数吧